Cálculo I: Números Reais

Neste post falaremos dos Números Reais e suas propriedades na introdução ao Cálculo.

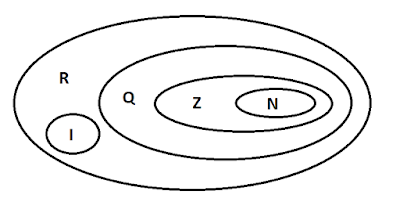
O conjunto dos números reais (ℝ) é formado pela união dos conjuntos Naturais (ℕ), Inteiros (ℤ), Racionais (ℚ) e Irracionais (𝕀).

No conjunto dos números Naturais (ℕ) existe uma propriedade importante, denominada Princípio da Indução Finita (para mais detalhes, clique aqui). Essa propriedade é muito utilizada no estudo de sequências.

Com as propriedades existentes no conjunto dos ℝ, assim como no conjunto dos ℕ, ℤ e ℚ, é possível que se defina as operações de ADIÇÃO e MULTIPLICAÇÃO. Neste ponto definimos o que é um Corpo.

Definição 1: Um corpo é um conjunto M diferente de vazio que possui duas operações: ADIÇÃO ⊕ e MULTIPLICAÇÃO ⊗ de modo que satisfaça as seguintes propriedades:

a) Associativa: Dados a,b,c ∈ M são verdadeiras as seguintes relações:

(a ⊕ b) ⊕ c = a ⊕ (b ⊕ c)

(a ⊗ b) ⊗ c = a ⊗ (b ⊗ c)

b) Comutativa: Dados a,b ∈ M, são verdadeiras as seguintes relações:

a ⊕ b = b ⊕ a

a ⊗ b = b ⊗ a

c) Elemento neutro da adição: Deve existir 0 ∈ M tal que a ⊕ 0 = a, para todo a ∈ M.

d) Elemento neutro da multiplicação: Deve existir 1 ∈ M, tal que a ⊗ 1 = a, para todo a ∈ M.

e) Elemento simétrico ou oposto da adição: Deve existir -a ∈ M para cada elemento a ∈ M tal que:

a ⊕ (-a) = 0 (elemento neutro da adição).

f) Elemento inverso da multiplicação: Deve existir a⁻¹ ∈ M* para cada a ∈ M de forma que:

a ⊗ (a⁻¹) = 1 (elemento neutro da multiplicação)

g) Propriedade distributiva da multiplicação de uma adição: Para quaisquer elementos a, b, c ∈ M, deve ser válida a seguinte igualdade:

a ⊗ (b ⊕ c) = a ⊗ b ⊕ a ⊗c

De posse dessa definição temos que, dos conjuntos acima mencionados, apenas os conjuntos ℝ e ℚ satisfazem a definição acima para as operações de adição e multiplicação usuais e, portanto, podem ser chamados de Corpo.

---

Exercícios resolvidos:

Exercício 1: Mostre que o conjunto dos números Racionais (ℚ) forma um corpo segundo as operações de adição e multiplicação usuais:

O conjunto ℚ é formado por números que podem ser escritos por:

Onde tanto a quanto b são números Inteiros (ℤ), onde b ≠ 0.
Sejam os três números Racionais a seguir:

Vamos verificar as propriedades:

Propriedade a) Associativa:
Esta propriedade é válida para a soma e a multiplicação usuais já que, para quaisquer a,b,c,d,e,f ∈ ℤ são verdadeiras as igualdades:

Propriedade b) Comutativa:
Esta propriedade é válida para a soma e a multiplicação usuais já que, para quaisquer a,b,c,d ∈ ℤ são verdadeiras as igualdades:

Propriedade c) Elemento neutro da adição:
É válida pois o 0 pertence ao conjunto dos números Racionais.


Propriedade d) Elemento neutro da multiplicação:
É válida pois o 1 pertence ao conjunto dos números Racionais.

Propriedade e) Elemento simétrico ou oposto da adição:
É válida pois para qualquer elemento que pertença aos Racionais, o seu simétrico também pertence.

Propriedade f) Elemento inverso da multiplicação:
É válida pois para qualquer elemento que pertença aos Racionais, o seu inverso também pertence.

Propriedade g) Propriedade distributiva da multiplicação de uma adição:
É válida pois para qualquer elemento que pertença aos Racionais, a igualdade abaixo é verdadeira:

Por satisfazer todas as propriedades, temos que os números Racionais formam um corpo.

Exercício 2: Por que o conjunto dos números Naturais (ℕ) não é um corpo?
Por não possuir números negativos contata-se que a propriedade e) não pode ser cumprida. Além dela, a Propriedade f) também não.

Exercício 3: Por que o conjunto dos números Irracionais (𝕀) não é um corpo?

Por não possuir os números 0 e 1, não satisfaz as Propriedades c) e d).
Surge, destas propriedades, a seguinte Proposição:

Proposição 1: Para todo conjunto que seja um corpo, é verdadeiro:
1 - O elemento neutro é único;
2 - A unidade é única;
3 - Para cada elemento x do conjunto, existe um único elemento simétrico;
4 - Para cada elemento x do conjunto, existe um único elemento inverso multiplicativo;
5 - Se a,b,c pertencem ao conjunto de tal forma que a+b = a+c então, b = c;
6 - Dados a,b que pertençam ao conjunto, é verdadeiro:
-(-a) = a
-(a+b) = (-a) + (-b)
(-a)*b = a*(-b)
(-a)*(-b) = a*b
7 - Dados a,b que pertençam ao conjunto, é verdadeiro dizer que:
a*b = 0 se, e somente se, a = 0 ou b = 0
8 - Dados a,b que pertençam ao conjunto e sejam diferentes de zero, é verdadeiro dizer que:
(a⁻¹)⁻¹ = a
(a*b)⁻¹ = a⁻¹ * b⁻¹

Definição 2: Um corpo ordenado é um corpo K que possua um subconjunto P não vazio denominada conjunto dos números positivos de K, tal que:
a) Para todo a,b ∈ P tem-se que a+b e a*b ∈ P.
b) Para cada a ∈ K uma e somente uma das afirmativas abaixo é verdadeira:
ou a = 0, ou a ∈ P ou -a ∈ P

Definição 3: Seja C um corpo ordenado e seja S um subconjunto não vazio de C, define-se que:
a) S é limitado superiormente em C caso exista algum termo a ∈ C que seja maior ou igual a todos os termos de S. Dizemos nesse caso que a é uma cota superior de S em C. Se a for a menor cota superior de S em C, chamamos a de supremo de S em C.
b) S é limitado inferiormente em C caso exista algum termo b ∈ C que seja menor ou igual a todos os termos de S. Dizemos nesse caso que b é uma cota inferior de S em C. Se b for a menor cota inferior de S em C, chamamos b de ínfimo de S em C.
c) S é limitado em C quando possui cota inferior e superior em C.

---

Exercício resolvido:
Exercício 4: Mostre que o conjunto A = [3, 10) é limitado em ℝ.
De fato, basta tomarmos 2 ∈ ℝ e 15 ∈ ℝ, onde 2 é uma cota inferior e 15 é uma cota superior. No caso temos 3 como ínfimo de A em ℝ e 10 como supremo de A em ℝ.

---

Em outras palavras, o supremo de um conjunto é um valor tal que seja maior ou igual a todos os valores do conjunto porém não existe valor "intermediário" entre ele e o maior valor do conjunto. Esta afirmação só é verdadeira quando o supremo é o próprio maior valor do conjunto.
O raciocínio análogo ocorre para o ínfimo, devendo ser ele o menor valor do conjunto.

Definição 4: Um corpo ordenado completo é um conjunto tal que todo subconjunto dele, limitado inferiormente, admite ínfimo nele.

---

Exercício resolvido:
Exercício 5: Mostre que ℚ não é um corpo ordenado completo.
Dado o conjunto A = {x ∈ ℚ / x² > 2} temos que o ínfimo do conjunto √2 ∉ Q. Desta forma, este subconjunto de ℚ não possui ínfimo em ℚ, mas apenas em ℝ. (Veja também: Mostre que √2 não é Racional).

---

O conjunto dos ℝ é um corpo ordenado completo.

PS: O conjunto dos números Naturais pode ser definido com o 0 (zero) ou sem ele. Esta definição fica a critério do professor.

Calcule a soma: S = x + 2x² + 3x³ + ...

Progressão aritmético-geométrica

Neste exercício será calculada a soma da progressão aritmético-geométrica na qual o n-ésimo termo é dado por:

Solução:

A soma que se deseja calcular é:

Percebe-se que não se trata nem de uma progressão aritmética (PA) e nem de uma progressão geométrica (PG), mas um misto das duas.

Multiplicando a equação acima por x de ambos os lados temos:

Adotando a mesma estratégia para a obtenção da fórmula da soma da PG (veja aqui), faz-se a subtração:

Veja também:

Definição e exemplos do princípio da indução finita

Dedução das fórmulas de uma PG e explicação

Soma S = 1² + 2² + 3² + ... + n²

Somatório duplo

O que resulta em algo familiar já que do lado direito da igualdade temos a soma de uma PG com termo inicial a1 = x, razão q = x e n termos, exceto pelo último termo que esta subtraindo tudo. Assim, usando a fórmula da soma da PG que já é conhecida, obtemos:

Assim, dividindo tudo por (1-x) isolamos o Sn:

Perceba que este resultado vale apenas para x ≠ 1. Para x = 1 temos a soma de uma PA:

Limite fundamental exponencial (Euler)

Comprovação com uso da análise da existência do limite fundamental de Euler

Neste post será comprovada a existência do limite fundamental exponencial.

Para isto, será utilizado o seguinte teorema e a seguinte proposição:

O limite a ser calculado é dado por:

Assim, definimos

Temos que a função f(x) acima tem seu domínio no conjunto dos reais exceto o zero. Como queremos o limite para x tendendo ao infinito, então o zero não será um problema. Neste caso, podemos definir a sequência xn = n, onde n são números inteiros e portanto a sequência esta contida no domínio da função f(x), podendo ser aplicado o Teorema 1.

Desta forma:

Porém, como n é inteiro, podemos escrever f(n) em binômio de Newton na forma de uma série:

Para seguir com os cálculos é importante saber se f(n) é crescente ou decrescente, pois isso irá nos permitir concluir se existe o limite exponencial.

Sabemos que:

Agora, para verificar se é crescente ou decrescente, irei iniciar o estudo supondo que a função é crescente e assim, saber se isso é verdadeiro ou não. Se ela for crescente, então f(n) < f(n+1), ou seja:

Na etapa (3) acima, é possível verificar que o termos de dentro do somatório do lado esquerdo é negativo e portanto a desigualdade é verdadeira, o que garante que f(n) é crescente como suposto inicialmente.

Agora, um passo importante é saber se f(n) é limitado, ou seja, que existe um K tal que, para qualquer n, f(n) < K. Com isso, da Proposição 1, é possível garantir que f(n) converge.

Verificando se f(n) é limitada superiormente:

O somatório obtido acima é a soma de uma PG, que é facilmente calculado:

Logo, temos que f(n) é limitada superiormente e crescente, o que garante que o limite existe. O valor do limite não é possível ser calculado sem o uso de um software ou mesmo de recursos envolvendo derivada ou série de Taylor, que a meu entender são conteúdos que estão a frente destes aplicados aqui.

Porém, caso deseja-se calcular este limite, pode ser feito com o uso da regra de L'Hopital, por exemplo:

Substituindo a variável 1/x = y e após isso aplicando L'Hopital, temos:

O que é Integral?

Neste post será explicado o que é integral pela definição.

A integral nada mais é do que um somatório contínuo de áreas infinitamente pequenas.

Por exemplo:

Imagine o seguinte somatório discreto:

Neste caso, a soma é discreta pois há um intervalo entre cada fator. A distância entre o 4 e o 1, por exemplo, é de 3, o que não permite que esta soma seja contínua, mas sim discreta. Além disso, o somatório acima não é de áreas, e sim de pontos.

Agora imagine este mesmo somatório onde cada um dos fatores da soma representam a altura de um retângulo. Assim, se multiplicarmos cada um por uma largura, teremos um somatório de várias áreas. Neste caso, uma das possibilidades é adotarmos que a largura é o intervalo entre cada um dos i's. No caso acima o intervalo entre eles é 1. Assim, a soma fica:

O somatório acima é representado, graficamente, na figura a seguir.

O exemplo acima foi propositalmente mencionado pois ele é introdutório para que possamos calcular a integral da curva f(x) = x² para x variando de zero até 3. Neste caso, podemos adotar convenientemente dois tipos de retângulos. Um com diagonal em (i, 0) e (i + Δi , f(i + Δi)), que são os mostrados anteriormente, e retângulos com diagonal (i, 0) e (i + Δi , f(i)). Abaixo, os retângulos com suas diagonais para i variando de 1 em 1 até 3, além da curva, em vermelho, de f(x) = x²:

O cálculo da integral da curva f(x) é o cálculo da área abaixo da curva. Neste caso, podemos observar que a soma das áreas dos retângulos azuis é menor do que a área da curva, e a soma das áreas dos retângulos cinza, é maior. Temos, neste caso, a soma das áreas dos retângulos cinzas igual a 14, e dos retângulos azuis, 5. Porém, a medida que vamos diminuindo o intervalo entre os i's, a área da soma dos retângulos se aproxima da área da curva. Perceba como ficaria para o intervalo entre os i's sendo de 0,5.

Neste novo exemplo, a soma dos retângulos cinzas será de:
(0.5²)*0.5 + (1²)*0.5 + (1.5²)*0.5 + (2²)*0.5 + (2.5²)*0.5 + (3²)*0.5 = 11,375
E dos retângulos azuis:
(0²)*0.5 + (0.5²)*0.5 + (1²)*0.5 + (1.5²)*0.5 + (2²)*0.5 + (2.5²)*0.5 = 6,875

É fácil de perceber que os resultados ficaram mais próximos entre si e na figura é fácil notar que as áreas se aproximaram da área abaixo da curva. Fazendo o intervalo entre os i's sendo de 0,1, é muito mais fácil de perceber isso. Veja a seguir:

Como, neste caso, a base dos retângulos Δi = 3/nret = 3/30 = 0,1 (onde nret é o número de retângulos) e a altura é dada por k², onde k = i*Δi, sendo que para os retângulos cinzas i = 0,1,2,3,...,30 e para os retângulos azuis e i = 0,1,2,3,...,29. Desta forma temos:
Para os retângulos cinzas:

Podemos tirar para fora do somatório os termos não dependentes de i:

Porém, de acordo com o que já foi feito no blog, o somatório pode ser substituído por uma equação, conforme segue:

No caso do exemplo, basta substituir nret = 30 e temos:

Usando o mesmo raciocínio é possível mostrar que a área dos retângulos azuis é:

A medida que aumentamos nret a área dos retângulos tende à área abaixo da curva. Neste caso, a área abaixo da curva será o limite dos resultados obtidos acima, para nret tendendo ao infinito. É importante perceber que para nret tendendo ao infinito, tanto a área cinza quanto a azul será nove, já que os fatores que têm nret dividindo tenderão a zero.
Assim, obtemos o resultado da integral de f(x) = x² para 0 < x < 3.

Deve-se salientar que a integral não se define pela soma de áreas retangulares, mas sim de áreas infinitamente pequenas. O método adotado anteriormente usando retângulos foi apenas um artifício, é possível chegar ao mesmo resultado com métodos diferentes.

Outro exemplo que podemos usar este conceito é o do cálculo da área do círculo. Alguns autores alegam que a motivação para o cálculo integral surgiu pois os matemáticos não conseguiam calcular a área de um círculo. Assim, eles foram colocando vários polígonos regulares inscritos e circunscritos num círculo de raio 1. A medida que aumentava-se o número de lados dos polígonos, o polígono de dentro tinha uma área maior, e o de fora, menor, onde a área deles tendia a um limite, a área do circulo.

Polígonos com três, quatro, cinco, seis e quinze lados. Perceba que com 15 lados, os polígonos se aproximam bem do círculo, e consequentemente, suas áreas também.

O cálculo da área dos polígonos pode ser feito da seguinte forma (vou fazer o cálculo apenas do polígono inscrito, fazendo pelo circunscrito, certamente, teremos o mesmo resultado, e pode ficar como exercício para o leitor):

Sabe-se que a área de um triângulo pode ser obtida pelo produto de dois lado desse triângulo, multiplicado ao seno do ângulo entre eles dividido por dois.

Exemplo:

Um triângulo que tem dois lados medindo 5 e 8, e um ângulo entre eles de 45º, terá área de: (1/2)*(5*8*Sen(45°)) = 20 * √(2)/2 = 10 * √(2)

Neste caso, se traçarmos retas do centro da circunferência até cada vértice do polígono inscrito (cada traço desses mede o raio, percebe?) teremos vários triângulo iguais. Na verdade, o número de triângulos formado é igual ao número de lados do polígono. Ainda, o ângulo entre essas retas (esses lados de tamanho igual ao raio) é exatamente 360°/n (ou 2π/n em radianos), sendo n o número de lados do polígono. Ou seja, se o polígono é um triângulo, o ângulo entre as retas será de 120°.

Assim, a área do polígono será a soma da área dos triângulos, como o número de triângulos é 'n', e esses triângulos são formados por dois lados de medida igual ao raio e o ângulo entre esses lados é 360°/n, temos que a área do polígono será:

Fazendo o limite para n tendendo ao infinito e substituindo (1/n) por k, tal que se n tende ao infinito, k tende a zero, teremos (substituindo 360° por 2π radianos):

Como a parcela (r²/2) não depende de k, pode ser tirada pra fora do limite, ficando:

Porém, este limite não tem a forma dos limites conhecidos, mas é parecido com:

Basta aparecer 2*π multiplicando k embaixo, e chamamos 2*π*k = x, que teremos o limite acima, que é conhecido.

Assim:

Que é exatamente o valor da área do círculo.

Claro que naquela época eles não conheciam a medida de ângulo em radianos, já que eles nem conheciam o valor de π - passaram a conhecer depois de descobrir a área do círculo. Na verdade, o valor de π é até hoje desconhecido na sua plenitude, pois ele, aparentemente tem infinitas casas depois da vírgula e não é periódico. Uma forma de se aproximar a ele é fazendo este limite acima para um polígono de muitos lados. Mas utilizando a medida em radianos e o conhecimento de limite podemos perceber que a conta esta correta.

Exercício Resolvido - Somatório de N² = 1² + 2² + 3² + ... + n² ou ∑(n^2) = 1^2 + 2^2 + 3^2 + ... + n^2

Ache uma equação para calcular o somatório de N² = 1² + 2² + 3² + ... + n², sendo n um número inteiro.

Solução:

O cálculo de ∑n² pode ser feito de várias formas. Tentarei demonstrar algumas:

1º método:

Sabendo que:

(n+1)³ - n³ = (n³ + 3n² + 3n + 1) - n³ = 3n² + 3n + 1

Assim:

∑[(p+1)³ - p³] = ∑[3p² + 3p + 1]

Mas:

∑[(p+1)³ - p³] = (2³ - 1³) + (3³ - 2³) + ... + [(n+1)³ - n³]

Perceba que o primeiro termo de cada parênteses é cancelado com o segundo do parênteses seguinte, sobrando apenas:

(n+1)³ - 1³

Então:

(n+1)³ - 1 = ∑[3p² + 3p + 1]

Mas:

∑[3p² + 3p + 1] = ∑3p² + ∑3p + ∑1 = 3*∑p² + 3*∑p + (1+1+1+1+1+...+1)

∑p = 1 + 2 + 3 + 4 + .. + n  -> (PA)

∑p = (1+n)*(n/2)

Temos também que:

∑1 = n

Assim:

(n+1)³ - 1 = ∑[3p² + 3p + 1]

(n+1)³ - 1 = 3*∑p² + 3*(1+n)*(n/2) + n

n³ + 3n² + 3n = 3*∑p² + 3n/2 + 3n²/2 + n

3*∑p² = n³ + 3n²/2 + n/2

∑p² = (1/6)*[2n³ + 3n² + n] = (1/6)*n*(n+1)*(2n+1)

2º método:

Usando o triângulo de Pascal:

Imagem retirada do livro Algorithmic Information heory, de G. Chaitin

Como o que queremos é o somatório:

1 + 4 + 9 + 16 + ... + n²

Se observarmos no triângulo acima a terceira coluna, o primeiro termo dela (1), é 1², se somarmos o primeiro ao segundo, temos 1+3 = 4, se somarmos o segundo ao terceiro, temos 3+6 = 9, o terceiro ao quarto 6+10 = 16 ....

Ou seja, a soma dois a dois dos termos da coluna, formam exatamente os termos da sequência que queremos:

Assim:

Ou, agrupado de forma melhor:

Mas, pelo teorema das colunas, que diz que:

Temos:

e

Tendo, por fim:

1² + 2² + 3² + 4² + ... + n² = (1/6)*n*(n+1)*(n-1 + n+2) = (1/6)*n*(n+1)*(2n+1)

3º método:

Digamos que a gente já conheça o resultado, mas desejamos provar que ele vale pelo método da indução finita :

Se n = 1:

1² = (1/6)*1*(1+1)*(2+1) = 1 Ok, é válido

Agora, a gente supõe que para n = k-1, a fórmula também é válida, admitimos então que:

1² + 2² + 3² + ... + (k-1)² = (1/6)*(k-1)*[(k-1)+1]*[2(k-1)+1] = (1/6)*(k-1)*k*(2k-1)

Supondo que a fórmula acima seja correta, devemos provar que vale para n = k também:

1² + 2² + 3² + 4² + ... + (k-1)² + k² = [(1/6)*(k-1)*k*(2k-1)] + k²

1² + 2² + 3² + 4² + ... + (k-1)² + k² = [(1/6)*(k²-k)*(2k-1)] + k²

1² + 2² + 3² + 4² + ... + (k-1)² + k² = [(1/6)*(2k³ - k² - 2k² + k)] + k²

Fazendo o mínimo múltiplo comum, ou seja, transformando k² = (6/6)*k² temos:

1² + 2² + 3² + 4² + ... + (k-1)² + k² = (1/6)*(2k³ - 3k² + k + 6k²) =

1² + 2² + 3² + 4² + ... + (k-1)² + k² = (1/6)*(2k³ + 3k² + k)

1² + 2² + 3² + 4² + ... + (k-1)² + k² = (1/6)*k*(k+1)*(2k+1)

que é a fórmula (1/6)*n*(n+1)*(2n+1) para n = k. Logo, esta provado por indução.

Progressão Geométrica (PG)

Dedução das fórmulas de uma PG e explicação

Dando continuidade às aulas, nada mais coerente do que, após uma aula de PA, a aula de PG.

Assim como a PA, a PG é uma sequência definida por um termo inicial, geralmente chamado de a₁ e uma razão, geralmente chamada de q.

Diferentemente da PA, na PG os termos da sequência são obtidos pelo produto do termo anterior pela razão, ou seja:

a₂ = a₁*q

a₃ = a₂*q = (a₁*q)*q = a₁*q²

a₄ = a₃*q = (a₁*q²)*q = a₁*q³

...

an = a(n-1)*q = a₁*q⁽ⁿ⁻¹⁾

Uma propriedade importante de observarmos é que o produto dos termos equidistantes ao termo central de um PG é sempre igual. Sendo mais claro:

Produto do primeiro termo com o último termo:

a₁*an = a₁*(a₁*q⁽ⁿ⁻¹⁾) = a₁²*q⁽ⁿ⁻¹⁾

Produto do segundo termo com o penúltimo termo

a₂*an-1 = (a₁*q)*(a₁*q⁽ⁿ⁻²⁾) = a₁²*q⁽ⁿ⁻¹⁾

Produto de terceiro termo com o antepenúltimo termo

a₃*an-2 = (a₁*q²)*(a₁*q⁽ⁿ⁻³⁾) = a₁²*q⁽ⁿ⁻¹⁾

...

Desta forma, fica fácil definir qual é o produto de todos os termos de uma PG. Veja só:

Produto = a₁*a₂*a₃*...*an. Como na multiplicação, a ordem dos fatores não altera o produto, podemos escrever esse produtório como:

Produto = (a₁*an)*(a₂*an-1)*(a₃*an-2)*... Como o valor dos produtos dentro dos parênteses é o mesmo (a₁²*q⁽ⁿ⁻¹⁾), como foi visto acima, e como esta sequência tem n termos, teremos (n/2) parênteses, já que cada parênteses tem dois termos. Assim:

Produto = [√(a₁²*q⁽ⁿ⁻¹⁾)]ⁿ = [a₁*√q⁽ⁿ⁻¹⁾]ⁿ.

Outro dado importante de se calcular, é a soma dos termos da PG. Existem várias formas de encontrar a fórmula da soma da PG (já foi feito neste blog por indução finita e soma telescópica), porém por ser de mais fácil compreensão, vou utilizar o método da soma telescópica (para quem não sabe o que é isso, vou explicar na medida que deduzo a fórmula)

O que queremos saber é a soma dos termos de uma PG, ou seja:

S = a₁ + a₂ + a₃ + ... + an

(1)     S = a₁ + a₁*q + a₁*q² + ... + a₁*q⁽ⁿ⁻¹⁾. Se multiplicarmos esse somatório por q, teremos:

(2) q*S = a₁*q + a₁*q² + a₁*q³ + ... + a₁*qⁿ

Agora vamos subtrair as equações (2) de (1), fazendo (2) - (1), assim teremos:

q*S - S = (a₁*q + a₁*q² + a₁*q³ + ... + a₁*qⁿ) - (a₁ + a₁*q + a₁*q² + ... + a₁*q⁽ⁿ⁻¹⁾)

Perceba que podemos anular vários termos que são iguais (este método é chamado de soma telescópica, onde você cancela vários termos iguais pela subtração por serem termos iguais).

Desta forma, todos os termos serão cancelado com exceção de (a₁*qⁿ) e a₁.

Assim:

q*S - S = (a₁*qⁿ) - (a₁). Isolando os termos comuns dos dois lados:

S*(q-1) = a₁*(qⁿ - 1), logo:

S = [a₁*(qⁿ - 1)] / [q-1], onde S é a soma dos termos.

Para uma PG decrescente infinita a fórmula é a mesma só que, para que a PG seja decrescente, q deve ser menor que 1 e maior que zero. Assim, como ela tende a ter infinitos termos, ou seja, n tende ao infinito, qⁿ vai tender a zero (faça o teste, pegue um valor qualquer, entre zero e 1 e eleve a potências grandes. Perceberá que quanto maior é este potência, mais o resultado se aproxima de zero. No infinito, será zero).

Assim, na PG infinita:

S = [a₁*(qⁿ - 1)] / [q-1], como qⁿ = 0

S = [a₁*(- 1)] / [q-1].

S = [-a₁] / [q-1]. Multiplicando o numerador e o denominador por (-1), o que não muda em nada a fração, temos:

S = a₁ / [1-q]

Abaixo, alguns exercícios e explicações que foram usados os conceitos citados acima:

Limite fundamental exponencial (Euler)

Dedução da fórmula de juros composto para parcelas iguais

Exercício Resolvido - Progressão geométrica (PG)

Exercício Resolvido - Divisão de somatórios.

Dada a tabela abaixo:

Calcule:

Solução:
Neste somatório, fi é o mesmo que Yi.
Para poder resolvê-lo, devemos calcular os dois somatórios individualmente, assim, o somatório do numerador será:
Y1X1 + Y2X2 + Y3X3 + Y4X4 + Y5X5 + Y6X6 =
= 3*10 + 5*11 + 9*15 + 10*19 + 2*21 + 1*26 = 478
O denominador fica:
Y1 + Y2 + Y3 + Y4 + Y5 + Y6 = 3 + 5 + 9 + 10 + 2 + 1 = 30

A resposta é: 478/30 = 15,9333...